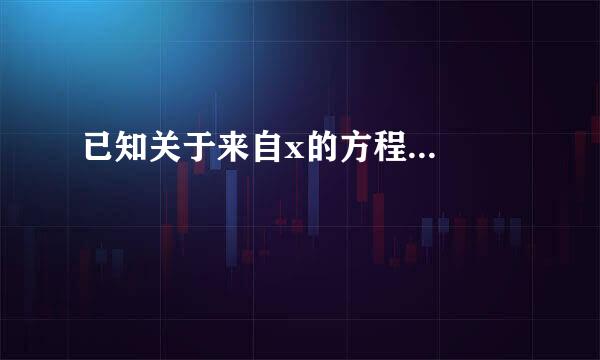
直线在圆上纯滚动时,直线上一点K的轨迹称为该圆的渐开线,该圆称为渐开线的基圆,直线称为渐开线的发生线。渐开线的形状仅取决于基圆的大小,基圆越小,渐开线越弯曲;基圆越大,渐开线越平直;基圆为无穷大时,渐开线为斜直线。渐开验土排图言线方程为:
x=r×cos(θ+α)+(θ+α)×r×sin(θ+α)
y=r×sin(θ+α)-(θ+α)×r比角造还副校引留明×cos(θ+α)

画法
已知圆的直径D来天飞巴解,画渐开线的方法如图
(1)将圆周分成若干等分(图中为12等分),将周长πD作相同等分;
(2)过周长上各等分点作圆的切线;
(翻数甲多3)在第一条切线上,自切点起量取周长的一个等分(πD/12)得点1;在第二条切线上,自切点起量取周长的两个等分(2xπD/12)得点2;依此类推得点3、4、……、12;
(4希犯波状几露保当明告)用曲线板光滑连接点1、2、3、……、12;即得圆的渐开线。