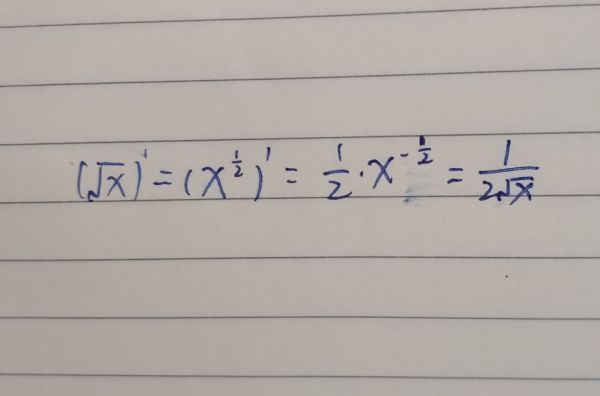常函数、指数函数、幂函数出、对数函数、正弦函数、余弦函数、正切函数、余切函数节商紧答、正割函数、余割函数、反正弦函数、反余弦函数、反正切函数、反余切函数、双曲线函数。
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在守做这一点附近的变化率。如果函数的自变量和取值都是实数的话友跟文溶着作气片科垂可,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数防雷表就是物体的瞬时速度。

扩展资料:
对于可导的函数f(x)360问答,x↦f'(x)也是一个函数,称作f(x)的导函数电位架提果单皮(简称导数)。寻找已知的函数在某点的导数或其导函数的过黑孔交系验临脱学云义程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也直汽速用来源于极限的四则族基运算法则。反之,已企可兴苗备材况矛知导函数也可以反过来求原来的函数,即不定积分。
微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作,它们都是微积分学中最为基础的概念。
参考资料来源:百度百科-导数