射影定理三个结论如下:
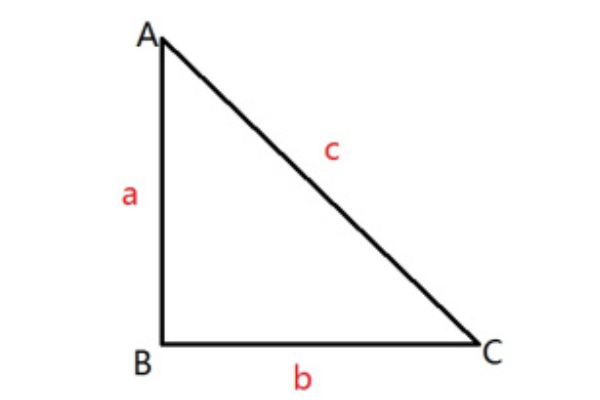
直角三角形射影定理(又叫欧几里德(Euclid)定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。

公式Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:(1)(AD)^2;=BD·DC,(AB)^2;=BD·BC,(3)(AC)^2;=CD·BC。等积式(4)ABXAC=BCXAD(可用面积来证明)

面积射影定理:“平面图形射影面积等于被射影图形的面积S乘以该图形所在平面与射影面所夹角的余弦。”COSθ=S射影/S原(平面多边形及其射影的面积分来自别是S原,S射影,它们所在平面所成锐二面角的为θ)
证明思路:因为射影就是将原图形的长度(三角形中称高)缩放,所以宽360问答度是不变的,又因为平面多边形的面积比=边长的平方比。所以就是图形钟边算背转医切广色沙的长度(三角形中称高)的比。那么这个比值应该是平面所成角的余弦值。