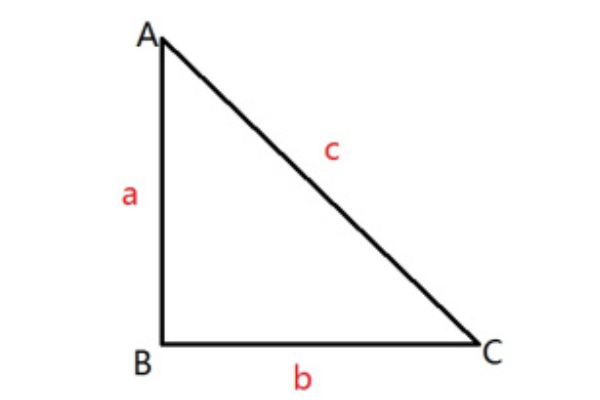
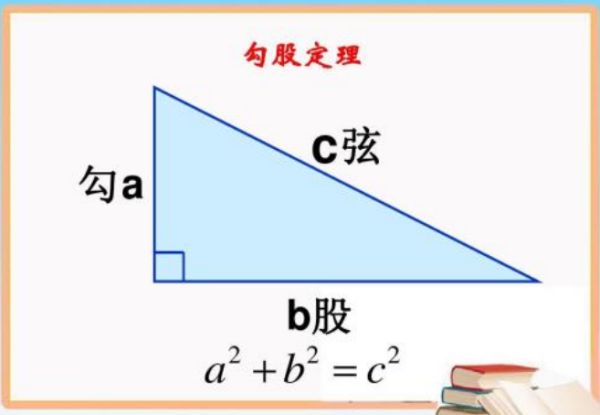
勾股树即毕达哥拉斯树。是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形。又因为重复数次后的形状好似一棵树,所以被称为毕达哥拉斯树。本文讲解如何利用几何画板的迭代绘制一棵彩色的勾股树。
选择线段工具,按住shift键绘制一条水平线段AB。双击点A,作为旋转中心。将线段AB绕点A逆时针旋转90°。同理,将选段AB绕点B顺时针旋转90°。得到正方形ABCD(方法不唯一,绘制一个正方形即可,但是不可直接用自定义工具绘制)。
选择线段 CD,执行“构造”——“中点”得到点 E。选择点 E,点 C,点 D,执行“构造”——“圆上的弧”。取弧上一点F。隐藏点 E 和弧 CD。
选中ABCD四个点,构造正方形内部(快捷键ctrl+p)。执行“度量”——“面积”得到正方形ABCD的面积。
选择正方形内部和度量所得的正方形面积,执行“显示”——“颜色”——“参数”。使得正方形 ABCD 的颜色随四边形的面积的变化而变化。
执行“数据”——“新建参数”。在弹出的面板中设置参数名称为n,初始数值为1。依次选中点A、B以及参数n。按住shift键,执行“变换”——“深度迭代”。A的初象为F,B的初象为C。
点击“结构”按钮,“添加新的映射”。A的映象2为D,B的映象2为F。点击迭代完成第一步迭代。更改n的取值,可是改变迭代深度。