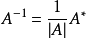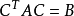jacky
正定矩阵
设M是n阶实系数对称矩阵，如果对任何非零向量 X=(x_1,...x_n)都有X′MX>0，就称M正定(Posit对应针植促侵iveDefinite)。 正定矩阵在相合变换下可化为标准型，即单位矩阵。 所有特征值大于零的对称矩阵（或厄米矩阵）也是正定矩阵。 另一种定义：一种实对称矩阵.正定二次型f(x1,x2,…,xn)=X′AX的矩阵A(A′)称为正定矩阵. 判定定理1：对称阵A为正定的充分必要条件是：A的特征值全为正。 判定定理2：对称赵值造雷应困满力最认事阵A为正定的充分必要条件是：A的各阶主子式都为正。 判定定理3：任意阵A为正定的充分必要条件是：A合同于单位阵。
