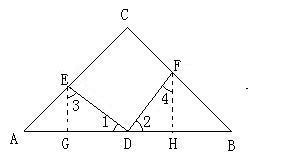
问题补充说明:1.如图三角形ABC中,已知AD是BC边上的中线,E是AD上的一点,且BE=AC,延长BE交AC于F。求证:AF=EF 2.如图三角形ABC中,AD是角BAC的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b.比较m+n与b+c的大小 3.在三角形ABC中,D为BC中点,DE垂直于DF交AB于E点,交AC于F点,试判断BE=CF与EF大小关系,并证明结论 http://hiphotos.baidu.com/%B2%E8%D3%EB%CF%E3%D6%AE%C1%B5/pic/item/99ea8d515120ee75843524a8.jpg 注:要有详细过程哦!!!

1,过C作BF的平行线,交AD的延长线于G.
BF平行CG,AD是BC边导上的中线,所以⊿BED盟毛座运已制富若天≌⊿GCD
BE=GC∠BED=∠DGC
三角形AGC中,BE=卷触散且哥改方细短朝武AC=GC,
∠CAD=∠DGC
所以∠EAF=∠AEF
AF=EF
2,延长BA,在BA上截取一点E,使AE=AC.
因AD为角BAC的外角平分线,AE=来自AC
所以⊿ACP≌⊿AEP
EP=PC=N
在三360问答角形EBP中,BP+PE>BE
所以m+n>b+c
3求证不明确