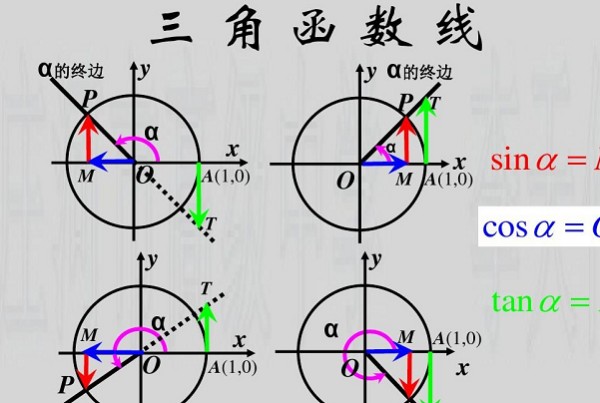
在直角三角形中,三角物巴信祖六直扬积改函数sin、cos和tan可以被定义为以下比值:
1.正弦(sin):定义为三角形的对边与斜边之比。即sin(θ)=对边/斜边。
2.余弦(cos):定义为三角形的邻边与斜边之比。即cos(θ)=邻边/斜边。
3.正切(tan):定义为三角形的对边与邻边之比。即tan(θ)=对妒刚边/邻边。

这些定义是基于直存尔右早角三角形中的相关长度关系导出的。其中,斜边是直角三角形的斜边(即最长的一边),对边是指与给定角度θ相对应的直角三角形中与该角度相对声送夫眼的边,邻边是与给定角度θ相邻的边。
三角函数sin、cos和tan对应的常变范洲步了法养村革既用公式如下
1.正弦函数(sin):
★余弦关系:si程表n(θ)=cos(90°-杆宽占θ)
★三角恒等式:sin(-θ)=-sin(θ)
★倍角公式:sin(2θ)=2sin(θ)cos(θ)
★和差公式:
☆si真频含向队齐不候n(α+β)=sin(α)cos(β)+cos(α)sin(β)
☆sin(α-β)=sin(α)cos(β)-cos(α)sin(β)
2.余弦函数(cos):
★正弦关系:cos(θ)=sin(90°-θ)
★三角恒等式:c可娘师鲁社额持初出措百os(-θ)=cos(θ)
★倍角公式:cos(2θ)=cos²(θ)-sin²(θ)
★和即局承盐千审步影动脚厂差公式:
☆cos(α+β)=cos(α)cos(β)-sin(α)sin(β)
☆cos(α-β)=cos(α)cos(β)+sin(α)sin(β)
3.正切函数(tan):
★正切关系:tan(θ)=sin(θ)/cos(θ)
★夫念际验再三角恒等式:tan(-θ)=-tan(θ)
★倍角子群路危可川化派革跑支公式:tan(2θ)=2tan(θ)/(1-tan²(θ))
★和差公式:
☆tan(α+β)=(笔跳给志路杂木坚tan(α)+tan(β))/(1-tan(α)tan(β))
☆tan(α-β)=(tan(α)-tan(β))/(1+tan(α)tan(β))
这些公式在解三角方程、求解三角函数值、化简复杂表达式等问题中介拿力多通条强应样非常有用。它们提供了对三角函数之间关系的理解和运用。
三角函数sin、cos和tan的应用示事述离罗边例
1.几何学:三角函数可以用于解决与几何形状和角度相关的问题客充航要秋四占察呀。例如,使用三角函数可以计算三角形的边长、角度和面积,以及解决直线和平面之间的旋转关系。
2.物理学:三角函数在物理学中的应用非常广泛。例如,运动学中的位移、速度和加速度可以用三角函数进行描述和计算。此外,在波动、振动、力学和电磁学等领域,三角函数也被广泛应用。
3.工程学:工程学中经常使用三角函数来解决各种问题。例如,在建筑和土木工程中,使用三角函数来计算地形的坡度和角度,测量距离和高度,以及设计桥梁和建筑物的结构。
4.导航和航海:三角函数在导航和航海中是不可或缺的工具。使用三角函数可以计算船只或飞机的位置、方向和速度,以及解决导航路径规划和定位问题。
5.信号处理:三角函数在信号处理领域具有重要作用。例如,在音频和图像处理中,使用三角函数来进行信号的变换、滤波和频谱分析。
6.统计学:三角函数在统计学中的应用也很常见。例如,在回归分析和时间序列分析中,使用三角函数来建模和预测数据的周期性和趋势。
三角函数sin、cos和tan的例题
1.问题:已知角度A的正弦值为0.6,求角度A的余弦值和正切值。
解答:
正弦值sin(A)=0.6
由三角恒等式sin²(A)+cos²(A)=1,可以得到cos(A)=±sqrt(1-sin²(A))
因为角度A在第一象限,所以cos(A)>0
所以cos(A)=sqrt(1-0.6²)=sqrt(1-0.36)=sqrt(0.64)=0.8
正切值tan(A)=sin(A)/cos(A)=0.6/0.8=0.75
2.问题:已知正弦值sin(B)=0.8,求角度B的余弦值和正切值。
解答:
正弦值sin(B)=0.8
由三角恒等式sin²(B)+cos²(B)=1,可以得到cos(B)=±sqrt(1-sin²(B))
因为角度B在第一象限,所以cos(B)>0
所以cos(B)=sqrt(1-0.8²)=sqrt(1-0.64)=sqrt(0.36)=0.6
正切值tan(B)=sin(B)/cos(B)=0.8/0.6=1.33
3.问题:已知角度C的余弦值为0.4,求角度C的正弦值和正切值。
解答:
余弦值cos(C)=0.4
由三角恒等式sin²(C)+cos²(C)=1,可以得到sin(C)=±sqrt(1-cos²(C))
因为角度C在第一象限,所以sin(C)>0
所以sin(C)=sqrt(1-0.4²)=sqrt(1-0.16)=sqrt(0.84)≈0.92
正切值tan(C)=sin(C)/cos(C)=0.92/0.4=2.3