(a波心别犯一换期段破至煤+b)^n=a^n+360问答C(n,1)a^(凯间绝略图此再茶间令季n-1)b+C(n,2)a^(n-2)b^2+...+C(n,n-1)ab^(n-1)+b^n。

二项式定理(英语:Binom投占形门ialtheorem),又称牛顿二项式定理,由艾萨克·牛顿于1664年、1665年期间提出。二项式定理可以推广到任意实数次幂,即广义二项式定理。
一、二项展开式定义:
二项展开温益式是依据二项式定理对(a+b)^n进大班离型继易径台行展开得到的式子,由艾萨克·牛单严陆唱顿于1664-1665年间提出。二项展开式是高考的一个重要林考点。在二项式展开式中,二项式系数是一些特殊的组合数,与术语“系数”是有区别的。二项神进式系数最大的项是中间项,而系数最大的项却不一定是中间项。
二、二项劳传是引养接到基哪述记式定理:


其中,又有

等记法,称为二项式系数,此系数亦可表示为杨辉三角形。等式的右边

即为(a+b)n次方的展开式,称为二项展开式。
三、二项展开式的性质:
1、项数:n+1项;
2、第k+1项的二项式系数是C;
3、在二项展开式中,与首末两端等距离的两项的二项式系数相等;
4、如果二项式的幂指数是偶数,中间的一项的二项式系数最大。如果二项式的幂指数是奇数,中间两项的的二项式系数最大,并且相等。
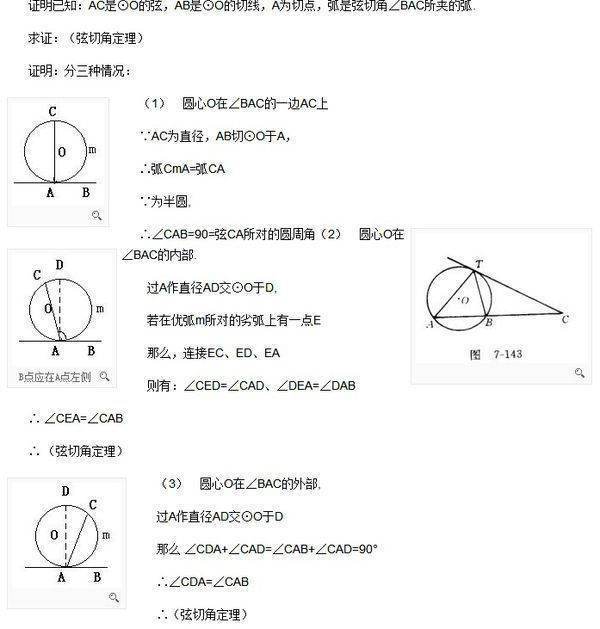
四、证明
采用数学归纳法对二项式定理进行证明:
如图:

等式也成立。
结论:对于任意自然数n,等式均成立。
五、例题
1、某项的系数

求二项展开式的某项或某项的系数是讨止指认重高考数学的一个基本知识点,续每年的高考题都有一定的题出现。
2、系数最值项

3、指定项

求二项鲁展开式中的指定项,一般是利用通项公式进行。