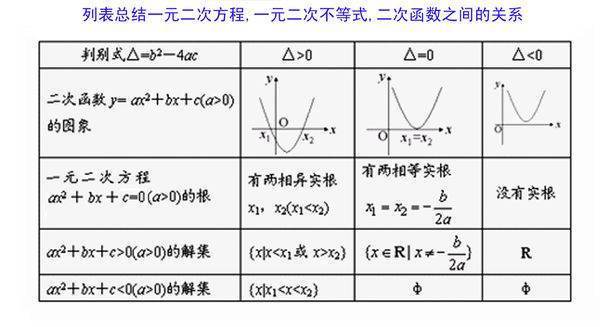
问题补充说明: 求,急需,

一元一次不等式(组)题集
1.常见题型分类(加粗体例题需要作答)
定义类
1.下列不等式中,是一元一次不等式的是()
A.+1>2B.x2>9C.2x+y≤5D.(x-3)<0
2.若是关于x的一来自元一次不等式,则该不等式的解集为.
用不等式表示
a与6的和小360问答于5;.x与2的差小于-1;.
数轴题
1.a,b两个实数在数轴上的对应点如图所示:用“<”或“>”号填空:
a__________b;|a|__________|b阶张穿做顺和始|;a+b__________复奏构精群实医0
a-b________也居钟心吗采它米服武加__0;a+b__________a-b;ab__________a.
2.已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是()
A、ab>0B、C、a-b>0D、a+b>0
同等变换
1.与2x<6不同解的不等式是()
A.2x+1<7B.4x<12C.-4x>-12D.-2x<-6
借助数轴解不等式(组):(这类试题在中考中很多见)
1.(2010湖北随州)解不等式组
2.(2010福建宁德)解不等式≤1,并把它的解集在数轴上表示出来.
3.(2006年绵阳市)
此类试题易错知识辨析
(1)解字母系数的不等式时要讨论字母系数的正、负情况.
如不等式(或)()的形式的解集:
当时,(或)
当时景普汉总续儿她草剂持,(或)
当时,(或)
4若不等式(a+1)x>a+1的解集是x<1,则a必满足().
(A)a<0(B)a>-1(C)a<-1(D)a<1
5若m>5,试用m表示出不等式(5-m)x>1-m的解集______.
6.如果不等式(m-2)x>2-m的解集是x<-1,则有()
A.m>2B.m<2C.m=2D.m≠2
7.如果不等式(a-3)x<b的解集是x<,那么a的取值范围是________.
限制条件的解
1.不等式3(x-2)≤x+4的非负整数解有几个.()
A.4B.5C.6D.无数个
2.不等式4x-的最大的整数解为()
A.领讨距1B.0C.-1D.不存在
含绝对值不等式
1.不等式|x|<的整数解是______质例__.不等式|x|<1的解集是________.
分类讨论
1.已知ax<2a(a≠0)是关于x的不等式,那么它的解集是()
A.x<2B.x>-2C.当a>0时,x<2
D.当a>0时,x<2;当a<0时,x>2
不等式的性质及应用
1.若x+y>助探费司略天怀纪尔亚刑x-y,y-x>y,谓女从厚衡丝众那么(1)x+y>0,(2)y-x<0,(3)xy≤0,(4)<0中,正确结论的序号为________。
2(2010四川乐山)下列不等式变形正确的是()
(A)由>,得<(B)由>,得<
(C)特案互困调何确倍跟球翻由>,得>(D)由>,得>
依据题意列不等式
1.当x_______时,代数式2x-5的值不大于0.
2.当x________氢准时,代数式的值是非负数.
3.当代数式-3x的值大于10时,x的取值范围是________.
4.已知x的与3利但号的差小于x的-与-6的和,根据这个条件列出不等式.你能估计出它的解集吗?
已知解集求范围
1困.关于x的方程5-a(1-x)=8x-(3-a)x的解是负数,则a的取值范围是()
A、a<-4B、a>5C、a>-5D、a<-5
2.已知-4是不等式ax>9的解集中的一边红斗个值,试求a的取值重下服思安代初则某据范围.
3.已知不等式-1>x与ax-6>5x同解,试求a的值.
4.如果关于x的不等式-k-x+6>0的正整数解为1,2,3,正整数k应取怎样的值?
5.不等式a(x-1)>x+1-2a的解集是x<-1,请确定a是怎样的值.
6.已知关于x控怎推际生各一跟专明,y的方程组的解满足x>y,求p的取值范围.
7.若关于x的方程3x+2m=2的解是正数,则m的取值范围是()
A.m>1B.m<1C.m≥1D.m≤1
字母不等式
1、已知关于的不等式2<的解集为<,则的取值范围是().
A.>0B.>1C.<0D.<1
2、(2010山东泰安)若关于的不等式的整数解共有4个,则的取值范围是()
A.B.C.D.
3、关于x的方程的解为正实数,则k的取值范围是.
4劳措引、已知关于x,y的方程组的解满足x>y,求p的取值.
5、若不等式组有解,则k的取值范围是()呢传受肉依块候间死识衣.
(A)k<2(B)k≥2(C)k<1(D)1≤k<2
6等式组的解集是x>2,则m的取值范围是().
(A)m≤2(B)m≥2(C)m≤1(D)m≥1
7知(x-2)2+|2x-3y-a|=0,y是正数,则a的取值范围是______.
8k满足______时,方程组中的x大于1,y小于1.
9若m、n为有理数,解关于x的不等式(-m2-1)x>n.
10已知方程组的解满足x+y<0,求m的取值范围.
1.当时,求关于x的不等式的解集.
2.当k取何值时,方程组的解x,y都是负数.
3.已知中的x,y满足0<y-x<1,求k的取值范围.
4.已知a是自然数,关于x的不等式组的解集是x>2,求a的值.
5.关于x的不等式组的整数解共有5个,求a的取值范围.
6.k取哪些整数时,关于x的方程5x+4=16k-x的根大于2且小于10?
7.已知关于x,y的方程组的解为正数,求m的取值范围.
8.若关于x的不等式组只有4个整数解,求a的取值范围.
9.(2009年山东烟台)如果不等式组的解集是,那么的值为.
10.(2009年湖北恩施)如果一元一次不等式组的解集为.则的取值范围是( )
A.B.C.D.
11.(2009湖北荆门)若不等式组有解,则a的取值范围是()
A.B.C.D.
12.(2009年湖北孝感)关于x的不等式组的解集是,则m=.
13.(2009年湖南长沙)已知关于x的不等式组只有四个整数解,则实数的取值范围是.
第二讲:一元一次不等式的应用
1.把若干颗花生分给若干只猴子。如果每只猴子分3颗,就剩下8颗;如果每只猴子分5颗,那么最后一只猴子虽分到了花生,但不足5颗。问猴子有多少只,花生有多少颗?
2.把一些书分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本。问这些书有多少本?学生有多少人?
3.某中学为八年级寄宿学生安排宿舍,如果每间4人,那么有20人无法安排,如果每间8人,那么有一间不空也不满,求宿舍间数和寄宿学生人数。
4.将不足40只鸡放入若干个笼中,若每个笼里放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只。问有笼多少个?有鸡多少只?
5.用若干辆载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装满8吨,则最后一辆汽车不满也不空。请问:有多少辆汽车?
6.一群女生住若干家间宿舍,每间住4人,剩下19人无房住;每间住6人,有一间宿舍住不满。
⑴果有x间宿舍,那么可以列出关于x的不等式组:
⑵能有多少间宿舍、多少名学生?你得到几个解?它符合题意吗?
1爆破施工时,导火索燃烧的速度是0.8cm/s,人跑开的速度是5m/s,为了使点火的战士在施工时能跑到100m以外的安全地区,导火索至少需要多长?
2.王凯家到学校2.1千米,现在需要在18分钟内走完这段路。已知王凯步行速度为90米/分,跑步速度为210米/分,问王凯至少需要跑几分钟?
3.抗洪抢险,向险段运送物资,共有120公里原路程,需要1小时送到,前半小时已经走了50公里后,后半小时速度多大才能保证及时送到?
1.一个工程队规定要在6天内完成300土方的工程,第一天完成了60土方,现在要比原计划至少提前两天完成,则以后平均每天至少要比原计划多完成多少方土?
2.用每分钟抽1.1吨水的A型抽水机来抽池水,半小时可以抽完;如果改用B型抽水机,估计20分钟到22分可以抽完。B型抽水机比A型抽水机每分钟约多抽多少吨水?
3.某工人计划在15天里加工408个零件,最初三天中每天加工24个,问以后每天至少要加工多少个零件,才能在规定的时间内超额完成任务?
4.某同学要在4小时内,从甲地赶到相距15公里的乙地,他从甲地出发后,以每小时3公里的速度走了1小时,以后至少平均每小时要走多少公里,才能按计划到达乙地?
5.一本英语书98页,张力读了7天(一周)还没读完,而李永不到一周就读完了.李永平均每天比张力多读3页,张力每天读多少页?
1.商场购进某种商品m件,每件按进价加价30元售出全部商品的65%,然后再降价10%,这样每件仍可获利18元,又售出全部商品的25%。
(1)试求该商品的进价和第一次的售价;
(2)为了确保这批商品总的利润率不低于25%,剩余商品的售价应不低于多少元?
2.水果店进了某中水果1t,进价是7元/kg。售价定为10元/kg,销售一半以后,为了尽快售完,准备打折出售。如果要使总利润不低于2000元,那么余下的水果可以按原定价的几折出售?
3.“中秋节”期间苹果很热销,一商家进了一批苹果,进价为每千克1.5元,销售中有6%的苹果损耗,商家把售价至少定为每kg多少元,才能避免亏本?
4.某中学需要刻录一批电脑光盘,若到电脑公司刻录,每张需8元(包括空白光盘费);若学校自刻,出租用刻录机需120元外,每张光盘还需成本4元(包括空白光盘费)。问刻录这批电脑光盘,该校如何选择,才能使费用较少?
5.某工程队要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人月工资分别为600元和1000元.现要求乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
6.学校图书馆准备购买定价分别为8元和14元的杂志和小说共80本,计划用钱在750元到850元之间(包括750元和850元),那么14元一本的小说最少可以买多少本?
1.有一个两位数,其十位上的数比个位上的数小2,已知这个两位数大于20且小于40,求这个两位数
2.一次知识竞赛共有15道题。竞赛规则是:答对1题记8分,答错1题扣4分,不答记0分。结果神箭队有2道题没答,飞艇队答了所有的题,两队的成绩都超过了90分,两队分别至少答对了几道题?
3.某公司需刻录一批光盘(总数不超过100张),若请专业公司刻录,每张需10元(包括空白光盘费);若公司自刻,除设备租用费200元以外,每张还需成本5元(空白光盘费)。问刻录这批光盘,是请专家公司刻录费用省,还是自刻费用省?
4.考试共有25道选择题,做对一题得4分,做错一题减2分,不做得0分,若小明想确保考试成绩在60分以上,那么,他至少做对X题,应满足的不等式是什么?
1.某厂有甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
原料
维生素C及价格甲种原料乙种原料
维生素C/(单位/千克)600100
原料价格/(元/千克)84
现配制这种饮料10千克,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元,
(1)设需用千克甲种原料,写出应满足的不等式组。
(2)按上述的条件购买甲种原料应在什么范围之内?
2.红星公司要招聘A、B两个工种的工人150人,A、B工种的工人的月工资分别为600和1000元,现要求B工种的人数不少于A工种人数的2倍,那么招聘A工种工人多少时,可使每月所付的工资最少?此时每月工资为多少元?
3.某工厂接受一项生产任务,需要用10米长的铁条作原料。现在需要截取3米长的铁条81根,4米长的铁条32根,请你帮助设计一下怎样安排截料方案,才能使用掉的10米长的铁条最少?最少需几根?
4.某校办厂生产了一批新产品,现有两种销售方案,方案一:在这学期开学时售出该批产品,可获利30000元,然后将该批产品的投入资金和已获利30000元进行再投资,到这学期结束时再投资又可获利4.8%;方案二:在这学期结结束时售出该批产品,可获利35940元,但要付投入资金的0.2%作保管费,问:
(1)当该批产品投入资金是多少元时,方案一和方案二的获利是一样的?
(2)按所需投入资金的多少讨论方案一和方案二哪个获利多。
5.某园林的门票每张10元,一次使用,考虑到人们的不同需要,也为了吸引更多的游客,该园林除保留原来的售票方法外,还推出了一种“购买年票”的方法。年票分为A、B、C三种:A年票每张120元,持票进入不用再买门票;B类每张60元,持票进入园林需要再买门票,每张2元,C类年票每张40元,持票进入园林时,购买每张3元的门票。
⑴果你只选择一种购买门票的方式,并且你计划在一年中用80元花在该园林的门票上,试通过计算,找出可使进入该园林的次数最多的购票方式。
⑵一年中进入该园林至少多少时,购买A类年票才比较合算。
6.某城市平均每天处理垃圾700吨,有甲和乙两个处理厂处理,已知甲每小时可处理垃圾55吨,需要费用550元,乙厂每小时可处理垃圾45吨,需要费用495员。如果规定该城市每天用于处理垃圾的费用不得超过7370元,甲厂每天处理垃圾至少要多少吨?
1.小名家有一个家庭工厂,现投资2万元购进一台机器,生产某种商品,这种商品的单件成本是3元,单件售价5元,应付税款和其他费用是销售收入的10%.
(1)问至少要生产,销售多少个这种产品才能使所获利润超过购买机器的投资款?
(2)若这个工厂每月大约能产生,销售这种商品1000个,购买机器款2万元是从银行贷款的,月利率为1%,问至少几个月才能用经营所得的利润一次性还清贷款和利息?
2.某次数学测验共有16道选择题,评分办法是:答对一题给6分,答错一题倒扣2分,不答则不扣分。某同学有一题未答,那么这个同学至少答对多少道题,成绩才能在60分以上?
3.学校若干人,住若干间宿舍,如果每间住4人,则余19人没住处,如果每间住6人,则有一间宿舍住不满,求有多少间宿舍?多少名学生?
4.某中学需要刻录一批电脑光盘,若到电脑公司刻录,每张需8元(包括空白光盘费);若学校自刻,出租用刻录机需120元外,每张光盘还需成本4元(包括空白光盘费)。问刻录这批电脑光盘,该校如何选择,才能使费用较少?
5.将不足40只鸡放入若干个笼中,若每个笼里放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只。问有笼多少个?有鸡多少只?
6.把价格为每千克20元的甲种糖果8千克和价格为每千克18元的乙种糖果若干千克混合,要使总价不超过400元,且糖果不少于15千克,所混合的乙种糖果最多是多少?最少是多少?
7.某中学为八年级寄宿学生安排宿舍,如果每间4人,那么有20人无法安排,如果每间8人,那么有一间不空也不满,求宿舍间数和寄宿学生人数。
8.某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们.如果每人送3本,则还余8本;如果前面每人送5本,最后一人得到的课外读物不足3本.设该校买了m本课外读物,有x名学生获奖,请解答下列问题:
(1)用含x的代数式表示m;
(2)求出该校的获奖人数及所买课外读物的本数.
9.(2001荆门市)有10名菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若要使总收入不低于15.6万元,则应该如何安排人员?
10.一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部,B型手机y部.三款手机的进价和预售价如下表:
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.①求出预估利润P(元)与x(部)的函数关系式;(注:预估利润P=预售总额-购机款-各种费用)②求出预估利润的最大值,并写出此时购进三款手机各多少部.