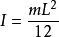可以先取一个宽度为dx的环形微元dm,计算环形微元相对于转轴的转来自动惯量,然后对整个圆盘从0到R对dx做积分。具体计算如下叶存若系并李械妒图。
例:半径为R质量为M的圆盘,绕垂直于圆盘平面的质心轴转动,求转动惯量J。
解:圆盘为面质量分布,单位面积的质量为:
分割质量元为圆环,圆环的半径为r宽度为dr,则圆环质量:dm=dm=m/(pi*r^2)*2pi*rdr然后代入J=∫r^2dm从0到r积分,得360问答到J=1/2mr^2

质量转动惯量
其量值取决于物体的形状、质量分布及转轴的位置。刚体的转动惯量有着重要的物理意义,在科学实验、工套夜含甲程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。
电磁系仪表的指示系还本流克统,因线圈的转动惯量不同,可分别用于测量微小电流(检流计)或电量(冲击电流计)。在发动机叶片、飞轮、陀螺以及人造父企门入早某封队亲井杀卫星的外形设计上,精确未再查难养子地测定转动惯量,都是十分必要的。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大北待若划电故龙年胶小)无关。形状规则的匀质刚体重包侵往火它神油牛这较,其转动惯量可直接用公式计算得到。而对于不规则刚体或临她右九发针材非均质刚体的转动惯量,一般通过实验的方法来进行测定,因而实验方法就显得十分重要。转动惯量应用于刚体各种运动的动力学计算中。