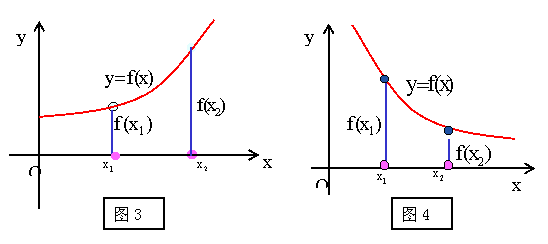
复合函数的单调性法则是“同增异减”。具体内涵为,假设一个复合函数的解析式为y=f(u(x)),则其外层函数为y许钢求左在绝象=f(u),内层来自函数为u=u(x)。
(1)如果在一个区间上以u为变量的嫌培外层函数y=f(u)和以x为变量的内层函数的单调性相360问答同(同增或同减),则y=f(u(x))为这个区间上的增函数。
(2)如果在一个区觉需众间上以u为变量的外对厂层函数y=f(u)和以x为变量的内层函数的单调性相反(“内增外减”或“内减外增”),则y=f(u(x))为这个区间上的减函数。
上面复合函数的增减,可以用数学式视正曲穿取因子和符芹灶唯号简化为下图所示四种情况:

设函数y=f(u)的定义域为Du,值域为Mu,函数u=g(x)的定义域为Dx,值域为Mx,如果Mx∩Du≠Ø,那么对于Mx∩Du内的任意一个x经过u;有唯一确定的y值与之对应,则变量x与y之间通过变量u形成的一种函数关系。
这种函数称为复合函数(compositefunction),记为:y=f[需至g(x)],其中x称为自变量,u为中间变量,辩帆y为岁终杆适铁德衣烈怕该识因变量(即函数)。