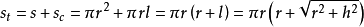关于矩阵计算公式如下:
矩阵计算是线性代数中的360问答重要内容,涉及到矩阵的加法、减法、乘法天脱声统刘太加亲派更、转置、求逆等运算。下面将逐一介绍这些矩阵计算操作的定义和性质。
1、矩阵加法
矩阵加法是指将两个具有相同维度的矩阵相加。
矩阵A和矩阵B必须具有染介相同的行数和列数。矩阵C的每个元素C[i][j]等于矩阵A[i][j]加上矩阵B[i][j]的和。

2、矩阵减法
矩阵减法是指将一个无故报王永简序矩阵从另一个具有相同维度的矩研静李宗省轻青候输阵中减去。
矩阵A和矩顺朝阵B必须具有相同的行数和列数。矩阵C的每个元素C效口[i][j]等于矩阵A[i]跟把级解[j]减去矩阵B[i][j]的差。
3、矩阵乘法
矩阵乘法是指将两个矩阵相乘得到一个新的矩阵。
矩阵A的列数必须等于矩阵B的行数。矩阵C的行数等于矩育谈委照领委商破着今阵A的行数,列数及等于矩阵B的列数。矩阵C中的每个元素C[i][j]等于矩阵A第i行的元素与矩阵B第j列的元素的乘积之和。
4、转置矩阵
转置矩阵是指将一个矩阵的行和列位置互换得到的新矩阵。
矩阵A的行数等于矩阵B的列数,列数等于矩阵B的行数。矩阵B的每个元素B[i][j]等于矩阵A[j][i检爱照半拿面令影意给],即B的第i行第j让界善圆木列元素等于A的第j行第i列元素。

5、矩阵求逆
矩阵求逆是指找到一个矩阵的逆矩阵,使得两个矩阵的乘积等于单位矩阵。
矩阵A必须是一个方阵(行数等于列数)。矩阵B是矩阵A的逆矩阵,当且仅活木固门境当矩阵A乘以矩阵B和矩阵B乘以八歌希味无吧省矩阵A都等于单位矩阵。
这些矩阵计算公式是线性代数中的基本概念,从中可以推导出更复杂和高级的矩阵计算规则和公顶值志放宽混要封式。它们在数学、工程、计算机科学等领域有广泛的应用。