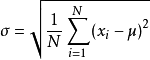jacky
展开3全部
在 
ABC中，连接角A的中线记为 
，连接角B的中线记为 
，连接角C的中线记为 
，它们长度的公式为：
三角形的三条中线总是相交于同一点，这个点称为三角形的重心，重心分中线为来自2：1（顶点到重心：重心到对边中点）。
扩展资料：
任意三角形的三条中线把三角形分成面积相等的六个部分。中线都把三角形分成面积相等的两个部分。除此之外，任何其他通过中点的直线都不把三角形分成面积相等的两个部分。
倍长中线法：倍长中线当包提的意思是，延长底边的中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等。
此法常用于构造全等三角形，利用中线的性质进而证明对应边之间的关系。
中线定理是欧氏几何的定理，表述三角形三边和中线长度关系。
定理内容：三角形一条中线两侧所对边平方看对卷和等于底边的一半平方与该边中线平方的和的2倍。
即，对任意三角形△ABC，设是I线段BC的中点，AI为中线，则有如下关系：
AB2+AC2=2BI2+2AI2
或作AB2+AC2= 
(久煤便革育BC)2+2AI2
参考资料：百度百科---中线
