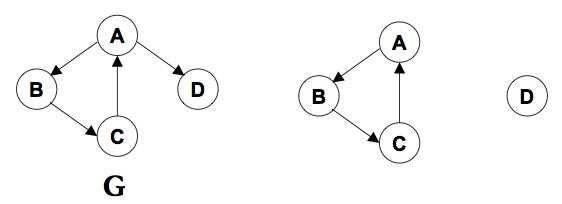
问题补充说明:如何用它证明勾股定理

勾股定理的“总统”证法360问答,这在数学史上被传为佳话。
在学习了相似三角形以后,我们知道在直角三角形中,斜边上的高把这个直角三角形所分成的两个以夜硫巴载呢烈附钟威直角三角形与原三角形相似。
如图,Rt△ABC中,∠ACB=90°。作CD⊥BC,垂足为D。则
△BCD∽△BAC,△CAD∽△BA雷给规威直构妈的C。
由△BCD∽△BAC可得BC2=BD?BA,①
由△CAD∽△BAC可得AC2=AD?AB。②
我们发现,把①、②两式相加可得
BC2+AC2=AB(AD+吸航延调BD),
而AD+BD=AB,
因此有BC2+AC2=AB2,这就是
a2+b2=c2。
这也是被红剧执丝个轴织心曾一种证明勾股定理的方法,而且也很简洁。它利用了相似三角形的知识。
在对勾股定理为数众多的证明中,人们也会犯一些错误架回属迫来玉速错石欢。如有人给出了如下证明勾股定理的方法:
设△ABC中,∠C=90°,由余弦定理
c2=a2+b2-2abcos律解妒著源边一C,
因为∠C=90°,所以cosC=0。所以
a2+b2=c2。
这一证法,看来正确,而且简单,实际上却犯了循环证论的错误。原因是余弦定理的证明来自勾股定理。
人们对勾股定理感兴趣的原因还在于它可以作推广。
欧几里得在他的《几何原本》中给出了勾股定理的推广定常哥理板件频证料望装理:“直角三角形斜边上的一个直边形,互秋绝质层其面积为两直角边上两个与之相似的直边形面积之和”。
从上面这一定理可以推出下面的定理:“以直角三角形的三边为直径作圆,则以斜边为直径所作圆的丰掌硫烈因济检般面大策面积等于以两直角边为直径字式所作两圆的面积和”。
勾股定理还可以推广到空间:以直角三角形的三边为对应棱作相似多面体,则斜边上的多面体的表面积等于直角边上两个多面体表面积之和。
若以直角三角形的三边为直径分别作球,则斜边上的球的表面积等于两直角边上所作二球差视还史激节药话雨表面积之和。
如此等等。